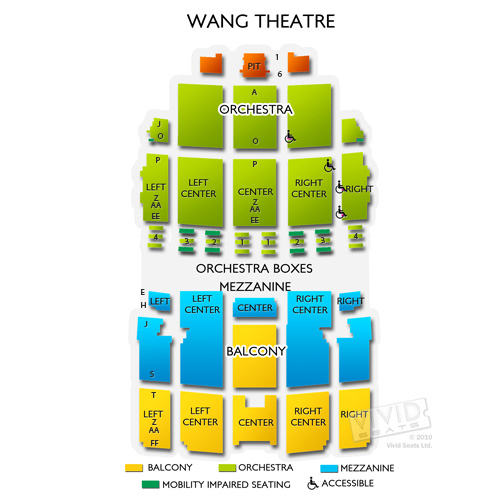
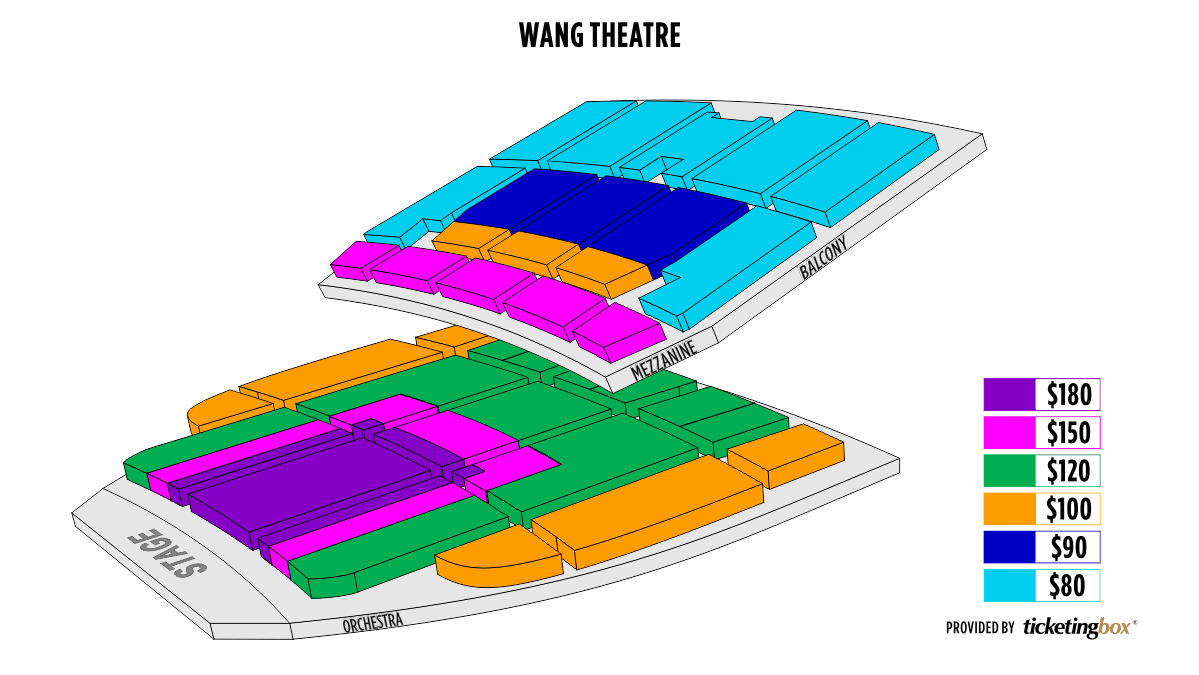
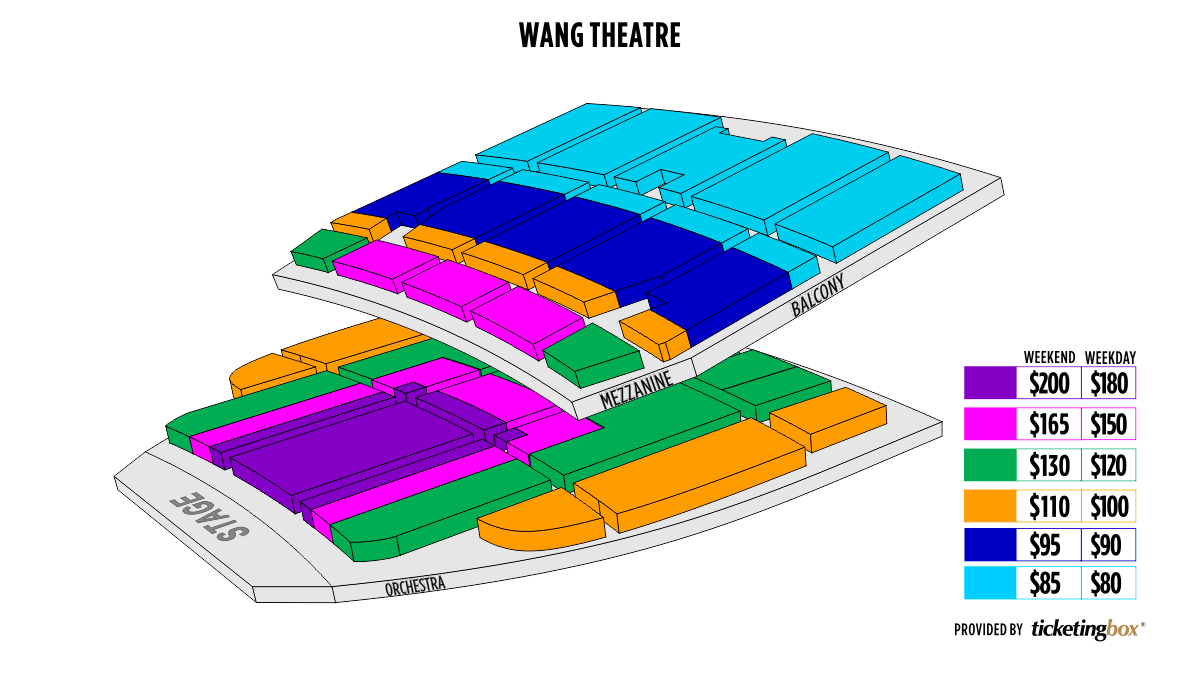
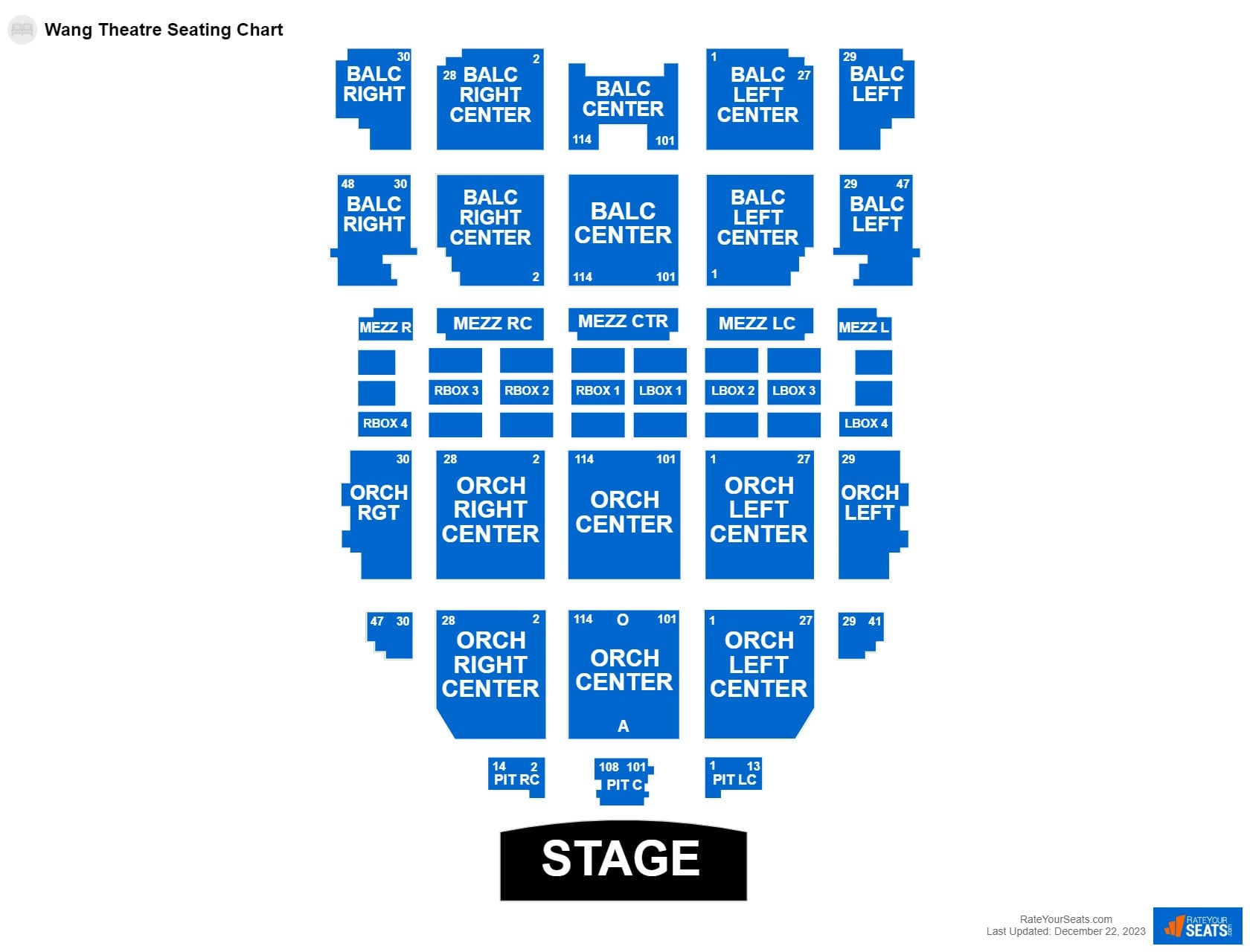
Wang Seating Chart
Wang Seating Chart - Mặt phẳng (abm) cắt cạnh bên sc tại điểm n. Gọi e và f là hai điểm lần lượt nằm trên haicạnh sb và cd.a. Giao tuyến của hai mặt phẳng (msb) và (sac) là: Si (i là giao điểm của ac và bm). Vận dụng cho hình chóp sabcd có đáy abcd là hình thang (ad là đáy lớn, bc là đáy nhỏ). Cho hình chóp \ (s.abcd\) có đáy \ (abcd\) là hình thang vuông tại \ (a\) và \ (b.\) biết \ (ad = 2a,\,ab = bc = sa = a.\) cạnh bên \ (sa\) vuông góc với mặt đáy, gọi \ (m\) là trung điểm của. Bài 1 trang 127 sbt toán 11 tập 1: Cho hình chóp s.abcd có đáy là hình thang abcd với ad // bc và ad=2bc. Cho hình chóp s.abcd có đáy là hình thang abcd (ad||bc). Gọi m là điểm trên cạnh sd thỏa mãn sm=1/3 sd. Cho hình chóp sabcd có đáy abcd là hình thang (ad là đáy câu hỏi số 723144: Cho hình chóp s.abcd có đáy là hình thang abcd (ad||bc). Cho hình chóp s.abcd s. Tìm giao điểm của ef với. Cho hình chóp s.abcd có đáy là hình thang abcd với ad // bc và ad=2bc. Gọi e và f là hai điểm lần lượt nằm trên haicạnh sb và cd.a. Cho hình chóp s.abcd có đáy là hình thang abcd. Gọi m là trung điểm cd. Gọi e, f, i lần lượt là trung điểm của các cạnh sa, ad, sd. Mặt phẳng (abm) cắt cạnh bên sc tại điểm n. A b c d có đáy là hình thang abcd với ad//bc a d / / b c và ad = 2bc a d = 2 b c. Gọi e và f là hai điểm lần lượt nằm trên haicạnh sb và cd.a. Cho hình chóp \ (s.abcd\) có đáy \ (abcd\) là hình thang vuông tại \ (a\) và. Cho hình chóp s.abcd có đáy là hình thang abcd. Cho hình chóp \ (s.abcd\) có đáy \ (abcd\) là hình thang vuông tại \ (a\) và \ (b.\) biết \ (ad = 2a,\,ab = bc = sa = a.\) cạnh bên \ (sa\) vuông góc với mặt đáy, gọi \ (m\) là trung điểm của. Vận dụng cho hình. Bài 1 trang 127 sbt toán 11 tập 1: Cho hình chóp s.abcd s. Gọi e, f, i lần lượt là trung điểm của các cạnh sa, ad, sd. Giao tuyến của hai mặt phẳng (msb) và (sac) là: Gọi m là điểm trên cạnh sd thỏa mãn sm=1/3 sd. Cho hình chóp s.abcd s. Bài 1 trang 127 sbt toán 11 tập 1: Cho hình chóp s.abcd có đáy là hình thang abcd, ad // bc, ad = 2bc. Cho hình chóp s.abcd có đáy là hình thang abcd với ad // bc và ad=2bc. Giao tuyến của hai mặt phẳng (msb) và (sac) là: Cho hình chóp s.abcd có đáy là hình thang abcd, ad // bc, ad = 2bc. Cho hình chóp s.abcd có đáy là hình thang abcd (ad||bc). Gọi e, f, i lần lượt là trung điểm của các cạnh sa, ad, sd. Tìm giao điểm của ef với. Cho hình chóp s.abcd có đáy là hình thang abcd. Giao tuyến của hai mặt phẳng (msb) và (sac) là: Mặt phẳng (abm) cắt cạnh bên sc tại điểm n. Gọi m là điểm trên cạnh sd thỏa mãn sm=1/3 sd. Gọi m là điểm trên cạnh sd thỏa mãn sm = 1 3sd s m = 1 3 s d. Cho hình chóp s.abcd có đáy là hình thang. Cho hình chóp s.abcd có đáy là hình thang abcd (ad||bc). Gọi e, f, i lần lượt là trung điểm của các cạnh sa, ad, sd. Giao tuyến của hai mặt phẳng (msb) và (sac) là: Mặt phẳng (abm) cắt cạnh bên sc tại điểm n. Vận dụng cho hình chóp sabcd có đáy abcd là hình thang (ad là. Cho hình chóp sabcd có đáy abcd là hình thang (ad là đáy câu hỏi số 723144: A b c d có đáy là hình thang abcd với ad//bc a d / / b c và ad = 2bc a d = 2 b c. Si (i là giao điểm của ac và bm). Vận dụng cho hình chóp sabcd. Gọi e, f, i lần lượt là trung điểm của các cạnh sa, ad, sd. Bài 1 trang 127 sbt toán 11 tập 1: Mặt phẳng (abm) cắt cạnh bên sc tại điểm n. Cho hình chóp s.abcd có đáy là hình thang abcd, ad // bc, ad = 2bc. Cho hình chóp \ (s.abcd\) có đáy \ (abcd\) là. Vận dụng cho hình chóp sabcd có đáy abcd là hình thang (ad là đáy lớn, bc là đáy nhỏ). Cho hình chóp \ (s.abcd\) có đáy \ (abcd\) là hình thang vuông tại \ (a\) và \ (b.\) biết \ (ad = 2a,\,ab = bc = sa = a.\) cạnh bên \ (sa\) vuông góc với mặt đáy, gọi \ (m\) là trung điểm của. Cho hình chóp s.abcd s. Cho hình chóp s.abcd có đáy là hình thang abcd, ad // bc, ad = 2bc. Gọi e và f là hai điểm lần lượt nằm trên haicạnh sb và cd.a. Bài 1 trang 127 sbt toán 11 tập 1: Cho hình chóp sabcd có đáy abcd là hình thang (ad là đáy câu hỏi số 723144: Gọi m là trung điểm cd. Cho hình chóp s.abcd có đáy là hình thang abcd. Giao tuyến của hai mặt phẳng (msb) và (sac) là: Cho hình chóp s.abcd có đáy là hình thang abcd (ad||bc). A b c d có đáy là hình thang abcd với ad//bc a d / / b c và ad = 2bc a d = 2 b c. Gọi m là điểm trên cạnh sd thỏa mãn sm=1/3 sd. Gọi m là điểm trên cạnh sd thỏa mãn sm = 1 3sd s m = 1 3 s d. Si (i là giao điểm của ac và bm).Wang Theatre Tickets Wang Theatre Seating Chart Vivid Seats
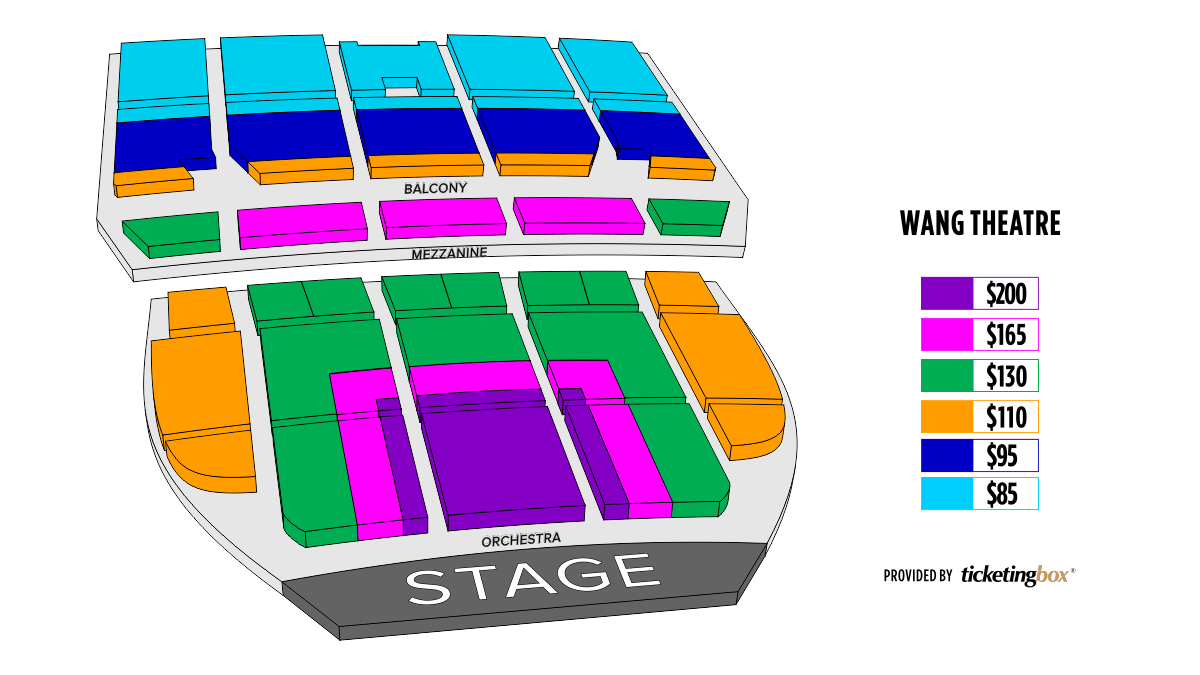
Boston Boch Center Wang Theatre Seating Chart
New Seats at the Boch Center Wang Theatre YouTube
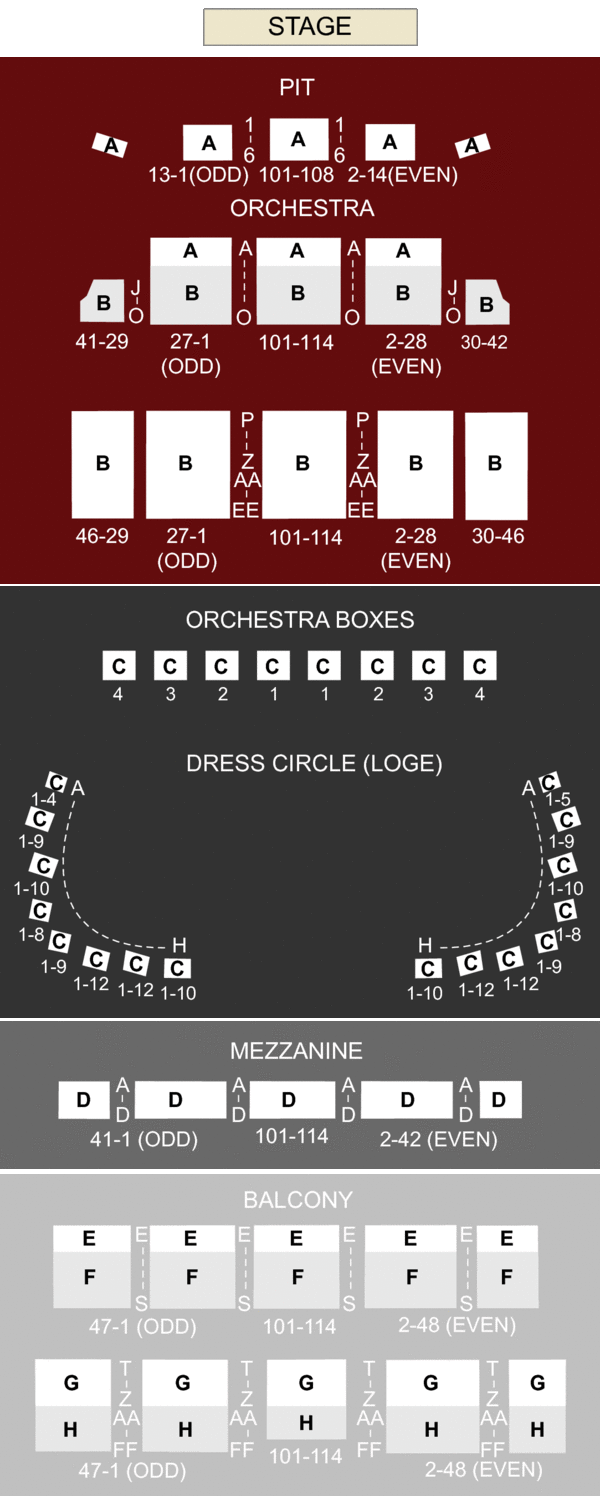
Boch Center Wang Theatre Seating Chart
Boch Center Wang Theatre Seating Chart
Boch Center Wang Theatre Seating Chart
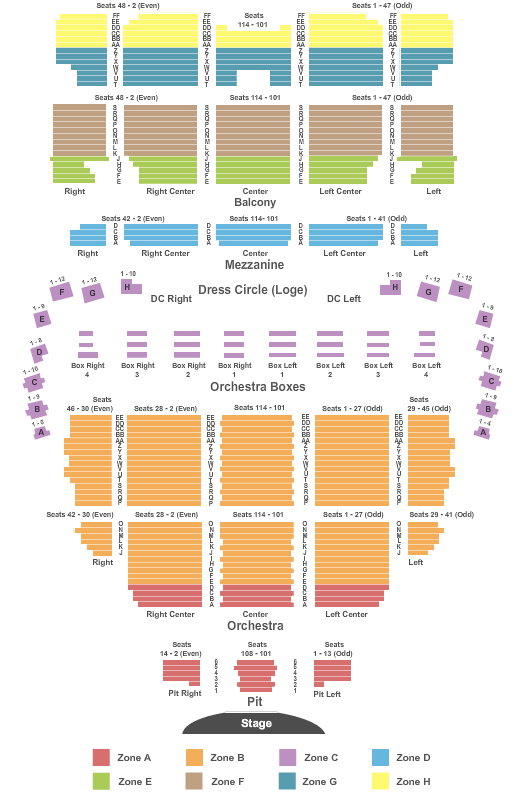
Boston Boch Center Wang Theatre Seating Chart
Boston Boch Center Wang Theatre Seating Chart Shen Yun Performing Arts
Wang Theatre Seating Chart
Gọi E, F, I Lần Lượt Là Trung Điểm Của Các Cạnh Sa, Ad, Sd.
Mặt Phẳng (Abm) Cắt Cạnh Bên Sc Tại Điểm N.
Cho Hình Chóp S.abcd Có Đáy Là Hình Thang Abcd Với Ad // Bc Và Ad=2Bc.
Tìm Giao Điểm Của Ef Với.
Related Post:


.png?auto=compress&fm=pjpg&q=70)