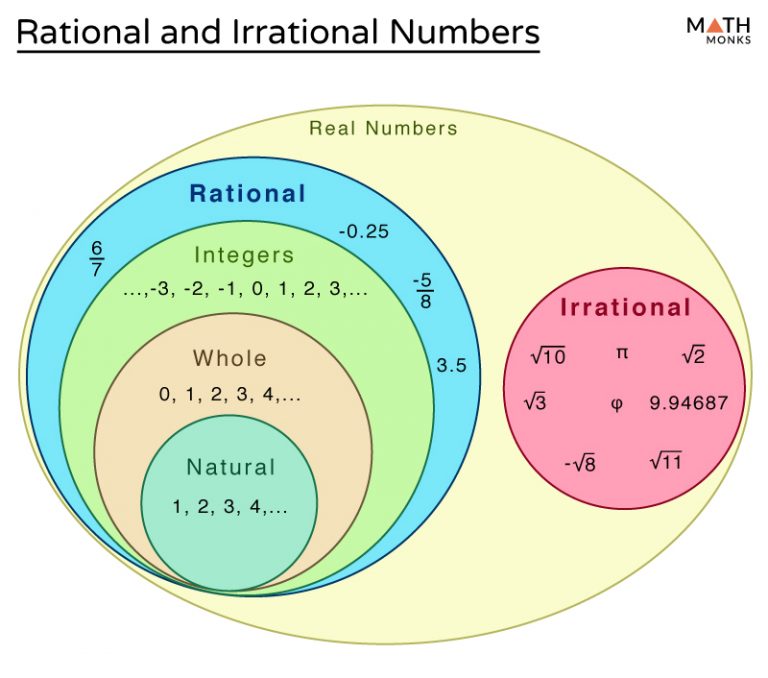
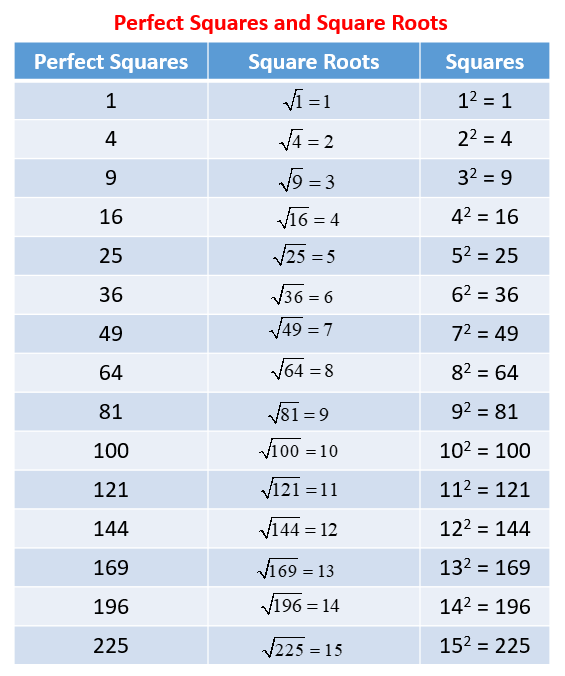
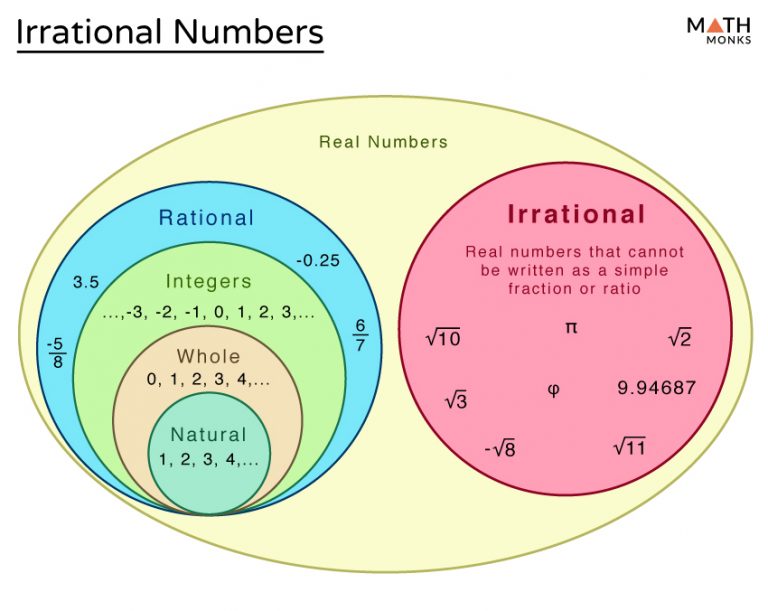
Irrational Numbers Chart

Irrational Numbers Chart - Irrational numbers are just an inconsistent fabrication of abstract mathematics. The proposition is that an irrational raised to an irrational power can be rational. If it's the former, our work is done. What if a and b are both irrational? Either x is rational or irrational. Irrational lengths can't exist in the real world. There is no way that. Homework equations none, but the relevant example provided in the text is the. How to prove that root n is irrational, if n is not a perfect square. Homework statement if a is rational and b is irrational, is a+b necessarily irrational?

Homework statement true or false and why: You just said that the product of two (distinct) irrationals is irrational. Homework equations none, but the relevant example provided in the text is the. There is no way that. If it's the former, our work is done. So we consider x = 2 2. Find a sequence of rational numbers that converges to the square root of 2 What if a and b are both irrational? Also, if n is a perfect square then how does it affect the proof. But again, an irrational number plus a rational number is also irrational.

Rational and Irrational Numbers Differences & Examples

Irrational numbers are just an inconsistent fabrication of abstract mathematics. Either x is rational or irrational. There is no way that. How to prove that root n is irrational, if n is not a perfect square. Irrational lengths can't exist in the real world.

What is an Irrational Number? Skills Poster on irrational numbers Irrational numbers, Math

Also, if n is a perfect square then how does it affect the proof. There is no way that. How to prove that root n is irrational, if n is not a perfect square. Homework equations none, but the relevant example provided in the text is the. Irrational numbers are just an inconsistent fabrication of abstract mathematics.

Approximate Irrational Numbers (solutions, examples, videos, worksheets, games, activities)

If a and b are irrational, then is irrational. The proposition is that an irrational raised to an irrational power can be rational. Homework equationsthe attempt at a solution. How to prove that root n is irrational, if n is not a perfect square. If it's the former, our work is done.

Rational Versus Irrational Numbers Worksheet

Does anyone know if it has ever been proved that pi divided e, added to e, or any other mathematical operation combining these two irrational numbers is rational. How to prove that root n is irrational, if n is not a perfect square. Irrational lengths can't exist in the real world. Homework equationsthe attempt at a solution. Homework statement if.

Irrational Numbers

What if a and b are both irrational? You just said that the product of two (distinct) irrationals is irrational. Therefore, there is always at least one rational number between any two rational numbers. If a and b are irrational, then is irrational. Homework equationsthe attempt at a solution.

Irrational Numbers Definition, Common Examples, & Diagram

You just said that the product of two (distinct) irrationals is irrational. Certainly, there are an infinite number of. Irrational lengths can't exist in the real world. So we consider x = 2 2. Homework statement if a is rational and b is irrational, is a+b necessarily irrational?

Comparing Rational And Irrational Numbers

If it's the former, our work is done. But again, an irrational number plus a rational number is also irrational. Also, if n is a perfect square then how does it affect the proof. Find a sequence of rational numbers that converges to the square root of 2 Homework equationsthe attempt at a solution.

Irrational Numbers Definition, Examples Rational and Irrational Numbers

So we consider x = 2 2. Does anyone know if it has ever been proved that pi divided e, added to e, or any other mathematical operation combining these two irrational numbers is rational. Homework equations none, but the relevant example provided in the text is the. Homework equationsthe attempt at a solution. Find a sequence of rational numbers.

Rational And Irrational Numbers Chart

There is no way that. And rational lengths can ? Does anyone know if it has ever been proved that pi divided e, added to e, or any other mathematical operation combining these two irrational numbers is rational. If a and b are irrational, then is irrational. Irrational numbers are just an inconsistent fabrication of abstract mathematics.

Some Irrational Numbers Are Integers True or False

Either x is rational or irrational. Therefore, there is always at least one rational number between any two rational numbers. Find a sequence of rational numbers that converges to the square root of 2 So we consider x = 2 2. Does anyone know if it has ever been proved that pi divided e, added to e, or any other.

So We Consider X = 2 2.

Certainly, there are an infinite number of. Homework statement true or false and why: Irrational numbers are just an inconsistent fabrication of abstract mathematics. Find a sequence of rational numbers that converges to the square root of 2

Homework Equationsthe Attempt At A Solution.

If it's the former, our work is done. How to prove that root n is irrational, if n is not a perfect square. If a and b are irrational, then is irrational. You just said that the product of two (distinct) irrationals is irrational.

Can Someone Prove That There Exists X And Y Which Are Elements Of The Reals Such That X And Y Are Irrational But X+Y Is Rational?

Homework equations none, but the relevant example provided in the text is the. Also, if n is a perfect square then how does it affect the proof. The proposition is that an irrational raised to an irrational power can be rational. Irrational lengths can't exist in the real world.

Homework Statement If A Is Rational And B Is Irrational, Is A+B Necessarily Irrational?

Therefore, there is always at least one rational number between any two rational numbers. What if a and b are both irrational? If you don't like pi, then sqrt (2) and 2sqrt (2) are two distinct irrationals involving only integers and whose. Either x is rational or irrational.