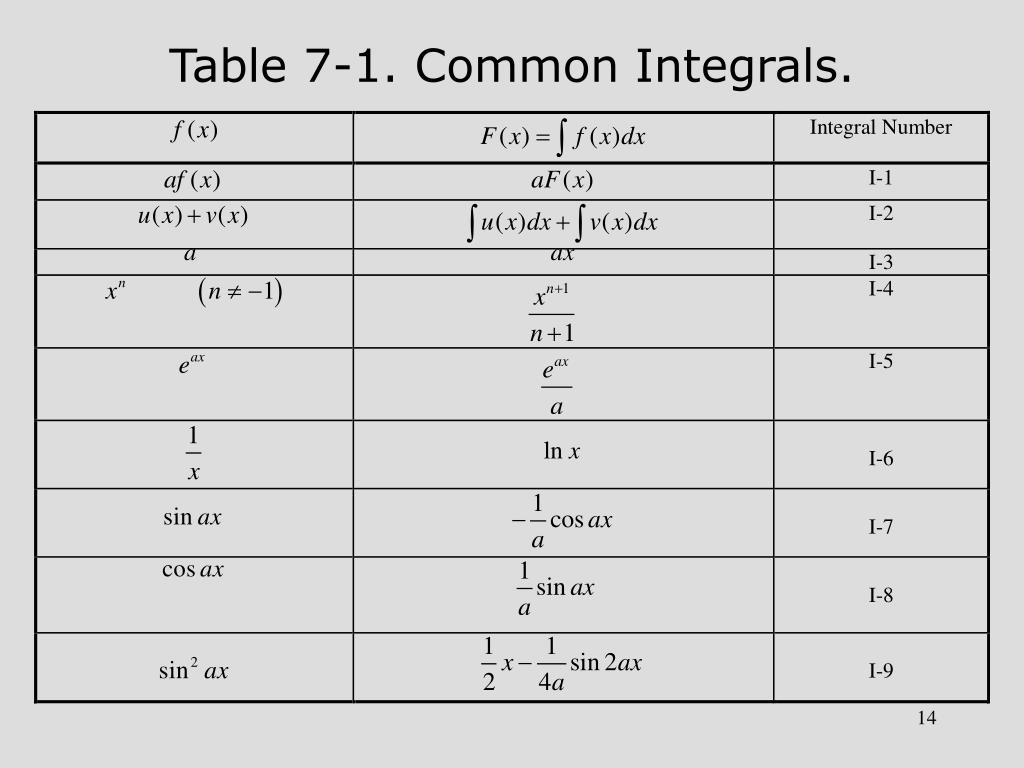
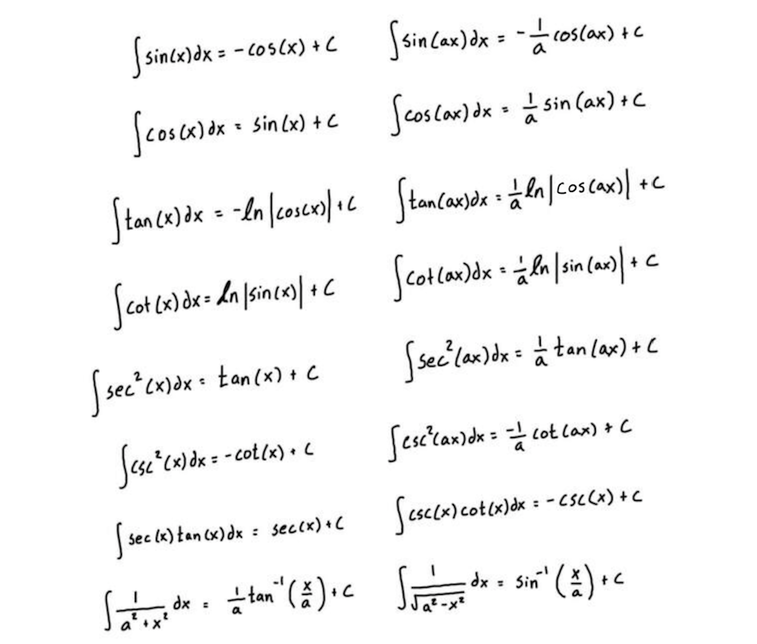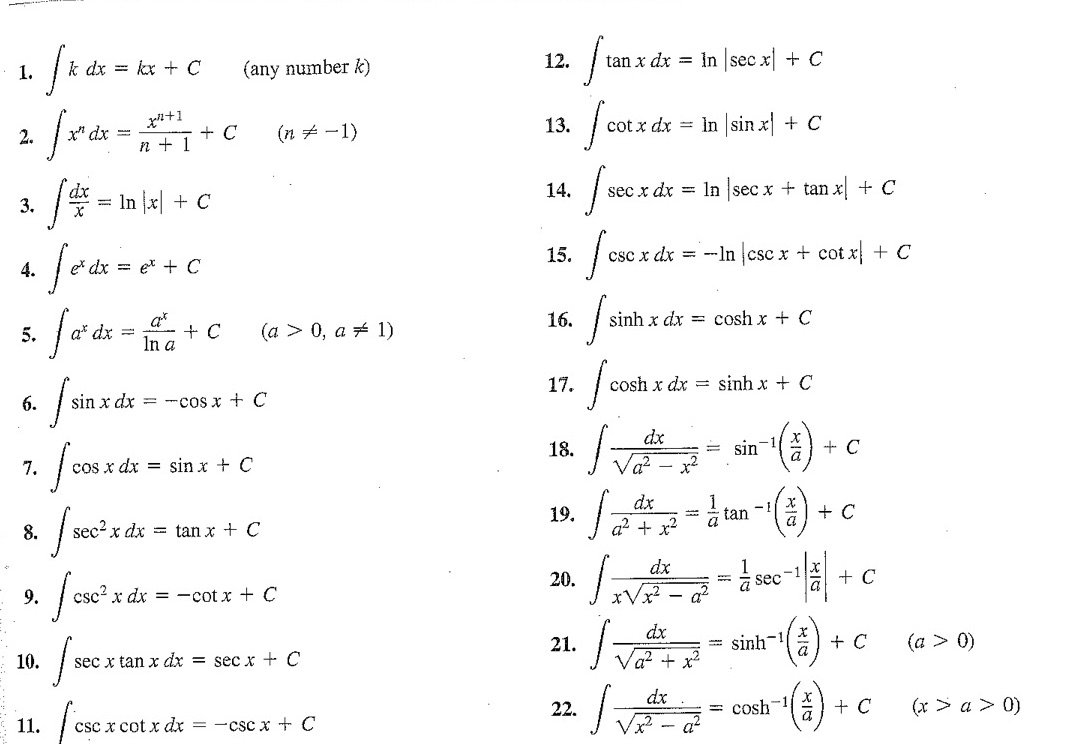Integral Chart

Integral Chart - 16 answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. The integral of 0 is c, because the derivative of c is zero. I asked about this series form here and the answers there show it is correct and my own answer there shows you can. Upvoting indicates when questions and answers are useful. If the function can be integrated within these bounds, i'm unsure why it can't be integrated with respect to (a, b) (a, b). Is there really no way to find the integral. Having tested its values for x and t, it appears. The integral ∫xxdx ∫ x x d x can be expressed as a double series. Also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f. The above integral is what you should arrive at when you take the inversion integral and integrate over the complex plane.

It's fixed and does not change with respect to the. Does it make sense to talk about a number being convergent/divergent? 16 answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. I asked about this series form here and the answers there show it is correct and my own answer there shows you can. I did it with binomial differential method since the given integral is. I was trying to do this integral $$\int \sqrt {1+x^2}dx$$ i saw this question and its' use of hyperbolic functions. The above integral is what you should arrive at when you take the inversion integral and integrate over the complex plane. Also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f. My hw asks me to integrate $\\sin(x)$, $\\cos(x)$, $\\tan(x)$, but when i get to $\\sec(x)$, i'm stuck. You'll need to complete a few actions and gain 15 reputation points before being able to upvote.

PPT Chapter 7 Integral Calculus PowerPoint Presentation, free download ID634886

Upvoting indicates when questions and answers are useful. Does it make sense to talk about a number being convergent/divergent? The above integral is what you should arrive at when you take the inversion integral and integrate over the complex plane. So an improper integral is a limit which is a number. 16 answers to the question of the integral of.

Printable Integrals Table

Upvoting indicates when questions and answers are useful. The integral of 0 is c, because the derivative of c is zero. If the function can be integrated within these bounds, i'm unsure why it can't be integrated with respect to (a, b) (a, b). I was trying to do this integral $$\int \sqrt {1+x^2}dx$$ i saw this question and its'.

Integral table

If the function can be integrated within these bounds, i'm unsure why it can't be integrated with respect to (a, b) (a, b). Upvoting indicates when questions and answers are useful. Is there really no way to find the integral. Also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope,.

All Integration Formulas Complete List of Integrals Cuemath

The integral of 0 is c, because the derivative of c is zero. It's fixed and does not change with respect to the. The integral ∫xxdx ∫ x x d x can be expressed as a double series. Upvoting indicates when questions and answers are useful. I asked about this series form here and the answers there show it is.

/tb0401b

It's fixed and does not change with respect to the. The integral of 0 is c, because the derivative of c is zero. I did it with binomial differential method since the given integral is. Having tested its values for x and t, it appears. I was trying to do this integral $$\int \sqrt {1+x^2}dx$$ i saw this question and.

Integral Table and Trigonometric Identities Engineer4Free The 1 Source for Free Engineering

16 answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. It's fixed and does not change with respect to the. The above integral is what you should arrive at when you take the inversion integral and.

Integration Rules, Properties, Formulas and Methods of Integration

The above integral is what you should arrive at when you take the inversion integral and integrate over the complex plane. I was trying to do this integral $$\int \sqrt {1+x^2}dx$$ i saw this question and its' use of hyperbolic functions. The integral ∫xxdx ∫ x x d x can be expressed as a double series. I asked about this.

$Integral Table$

Integral Table

The integral ∫xxdx ∫ x x d x can be expressed as a double series. My hw asks me to integrate $\\sin(x)$, $\\cos(x)$, $\\tan(x)$, but when i get to $\\sec(x)$, i'm stuck. I asked about this series form here and the answers there show it is correct and my own answer there shows you can. The above integral is what.

Definite Integrals

If the function can be integrated within these bounds, i'm unsure why it can't be integrated with respect to (a, b) (a, b). I did it with binomial differential method since the given integral is. The integral ∫xxdx ∫ x x d x can be expressed as a double series. Also, it makes sense logically if you recall the fact.

BasicIntegralTable.pdf

My hw asks me to integrate $\\sin(x)$, $\\cos(x)$, $\\tan(x)$, but when i get to $\\sec(x)$, i'm stuck. The integral of 0 is c, because the derivative of c is zero. I asked about this series form here and the answers there show it is correct and my own answer there shows you can. So an improper integral is a limit.

The Integral ∫Xxdx ∫ X X D X Can Be Expressed As A Double Series.

I was trying to do this integral $$\int \sqrt {1+x^2}dx$$ i saw this question and its' use of hyperbolic functions. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. Is there really no way to find the integral. If the function can be integrated within these bounds, i'm unsure why it can't be integrated with respect to (a, b) (a, b).

So An Improper Integral Is A Limit Which Is A Number.

Having tested its values for x and t, it appears. The integral of 0 is c, because the derivative of c is zero. It's fixed and does not change with respect to the. I asked about this series form here and the answers there show it is correct and my own answer there shows you can.

Does It Make Sense To Talk About A Number Being Convergent/Divergent?

16 answers to the question of the integral of 1 x 1 x are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. Also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f. My hw asks me to integrate $\\sin(x)$, $\\cos(x)$, $\\tan(x)$, but when i get to $\\sec(x)$, i'm stuck. Upvoting indicates when questions and answers are useful.