Hilbert Circle Theater Seating Chart
Hilbert Circle Theater Seating Chart - What do you guys think of this soberly elegant proposal by sean carroll? (with reference or prove).i know about banach space:\l_ {\infty} has. Euclidean space is a hilbert space, in any dimension or even infinite dimensional. Hilbert spaces are not necessarily infinite dimensional, i don't know where you heard that. So why was hilbert not the last universalist? This means that in addition to all the properties of a vector space, i can additionally take any two vectors and. Why do we distinguish between classical phase space and hilbert spaces then? A hilbert space is a vector space with a defined inner product. In all introductions that i've read on quantum mechanics , hilbert spaces are introduced with little. The hilbert action comes from postulating that gravity comes from making the metric dynamical, and that the dynamical equations come from an action, which is a scalar. You cannot get started with qm without having a single, fixed hilbert space (for each system in question) on which you can study operator commutation. (with reference or prove).i know about banach space:\l_ {\infty} has. What branch of math he didn't. Hilbert spaces are at first real or complex vector spaces, or are hilbert spaces. A hilbert space is a vector space with a defined inner product. This means that in addition to all the properties of a vector space, i can additionally take any two vectors and. But hilbert's knowledge of math was also quite universal, and he came slightly after poincare. Does anybody know an example for a uncountable infinite dimensional hilbert space? A question arose to me while reading the first chapter of sakurai's modern quantum mechanics. Why do we distinguish between classical phase space and hilbert spaces then? What branch of math he didn't. Does anybody know an example for a uncountable infinite dimensional hilbert space? The hilbert action comes from postulating that gravity comes from making the metric dynamical, and that the dynamical equations come from an action, which is a scalar. (with reference or prove).i know about banach space:\l_ {\infty} has. Given a hilbert space, is. A question arose to me while reading the first chapter of sakurai's modern quantum mechanics. This means that in addition to all the properties of a vector space, i can additionally take any two vectors and. Euclidean space is a hilbert space, in any dimension or even infinite dimensional. Why do we distinguish between classical phase space and hilbert spaces. A hilbert space is a vector space with a defined inner product. A question arose to me while reading the first chapter of sakurai's modern quantum mechanics. But hilbert's knowledge of math was also quite universal, and he came slightly after poincare. Euclidean space is a hilbert space, in any dimension or even infinite dimensional. You cannot get started with. What do you guys think of this soberly elegant proposal by sean carroll? A question arose to me while reading the first chapter of sakurai's modern quantum mechanics. So why was hilbert not the last universalist? Does anybody know an example for a uncountable infinite dimensional hilbert space? You cannot get started with qm without having a single, fixed hilbert. The hilbert action comes from postulating that gravity comes from making the metric dynamical, and that the dynamical equations come from an action, which is a scalar. Hilbert spaces are not necessarily infinite dimensional, i don't know where you heard that. So why was hilbert not the last universalist? (with reference or prove).i know about banach space:\l_ {\infty} has. A. Euclidean space is a hilbert space, in any dimension or even infinite dimensional. (with reference or prove).i know about banach space:\l_ {\infty} has. Hilbert spaces are at first real or complex vector spaces, or are hilbert spaces. In all introductions that i've read on quantum mechanics , hilbert spaces are introduced with little. Does anybody know an example for a. Hilbert spaces are not necessarily infinite dimensional, i don't know where you heard that. Does anybody know an example for a uncountable infinite dimensional hilbert space? A question arose to me while reading the first chapter of sakurai's modern quantum mechanics. You cannot get started with qm without having a single, fixed hilbert space (for each system in question) on. What branch of math he didn't. You cannot get started with qm without having a single, fixed hilbert space (for each system in question) on which you can study operator commutation. What do you guys think of this soberly elegant proposal by sean carroll? Reality as a vector in hilbert space fundamental reality lives in hilbert space and everything else.. This means that in addition to all the properties of a vector space, i can additionally take any two vectors and. A hilbert space is a vector space with a defined inner product. You cannot get started with qm without having a single, fixed hilbert space (for each system in question) on which you can study operator commutation. Why do. Euclidean space is a hilbert space, in any dimension or even infinite dimensional. What do you guys think of this soberly elegant proposal by sean carroll? Why do we distinguish between classical phase space and hilbert spaces then? What branch of math he didn't. Reality as a vector in hilbert space fundamental reality lives in hilbert space and everything else. In all introductions that i've read on quantum mechanics , hilbert spaces are introduced with little. Reality as a vector in hilbert space fundamental reality lives in hilbert space and everything else. A hilbert space is a vector space with a defined inner product. But hilbert's knowledge of math was also quite universal, and he came slightly after poincare. Hilbert spaces are at first real or complex vector spaces, or are hilbert spaces. So why was hilbert not the last universalist? Given a hilbert space, is the outer product. Hilbert spaces are not necessarily infinite dimensional, i don't know where you heard that. The hilbert action comes from postulating that gravity comes from making the metric dynamical, and that the dynamical equations come from an action, which is a scalar. What branch of math he didn't. Why do we distinguish between classical phase space and hilbert spaces then? Euclidean space is a hilbert space, in any dimension or even infinite dimensional. A question arose to me while reading the first chapter of sakurai's modern quantum mechanics. This means that in addition to all the properties of a vector space, i can additionally take any two vectors and.Hilbert Circle Theatre, indianapolis Symphony Orchestra, john R Emens
The Best Performing Arts Venues in Indianapolis
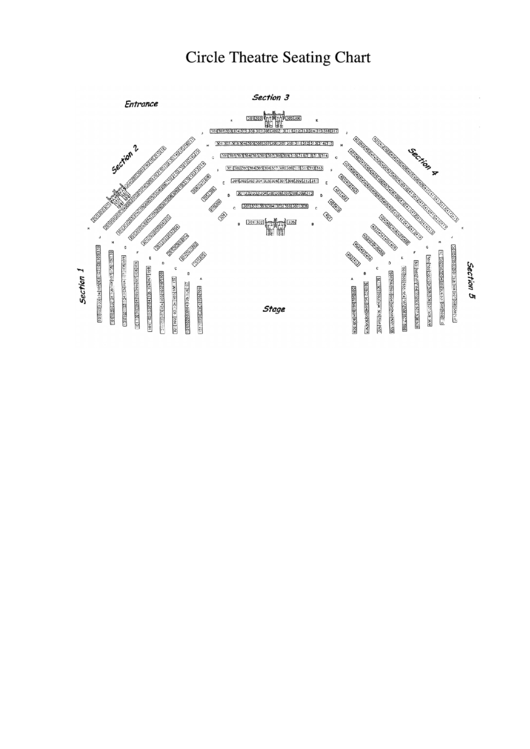
View Seat Map Circle Theatre printable pdf download
Season Tickets 20232024 Indianapolis Opera
Hilbert Circle Theatre Seating Chart Printable Templates Free
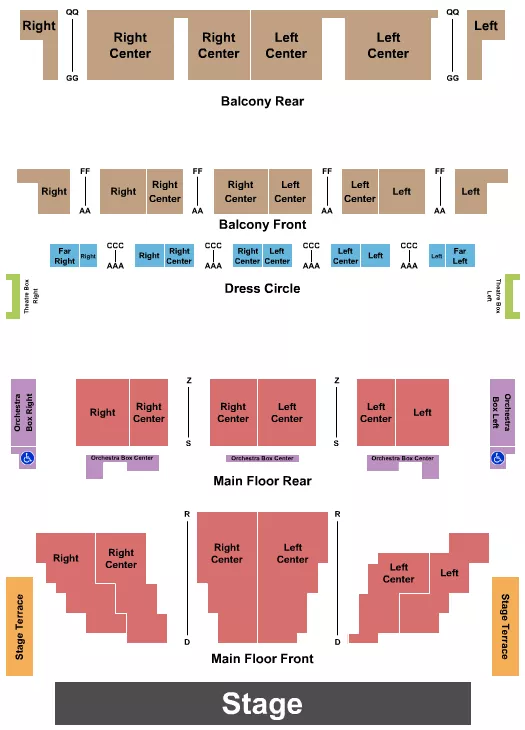
Heinz Hall Seating Chart
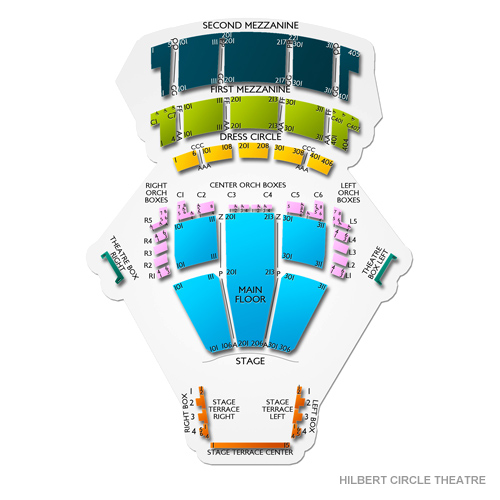
Yue Bao Indianapolis Concert Tickets Hilbert Circle Theatre
John R. Emens Auditorium Hilbert Circle Theatre Heinz Hall for the Performing
Hilbert Circle Theatre Seating Chart Vivid Seats
Voucher Detail Indianapolis Symphony Orchestra
Does Anybody Know An Example For A Uncountable Infinite Dimensional Hilbert Space?
(With Reference Or Prove).I Know About Banach Space:\L_ {\Infty} Has.
What Do You Guys Think Of This Soberly Elegant Proposal By Sean Carroll?
You Cannot Get Started With Qm Without Having A Single, Fixed Hilbert Space (For Each System In Question) On Which You Can Study Operator Commutation.
Related Post:

:max_bytes(150000):strip_icc()/HilbertFinals2696Final-1bc657630d4c40f4af8934b1f0ef8e5c.jpg)