Fourier Transform Chart
Fourier Transform Chart - This question is based on the question of kevin lin, which didn't quite fit in mathoverflow. Here is my biased and probably incomplete take on the advantages and limitations of both fourier series and the fourier transform, as a tool for math and signal processing. Derivation is a linear operator. What is the fourier transform? Fourier transform commutes with linear operators. Transforms such as fourier transform or laplace transform, takes a product of two functions to the convolution of the integral transforms, and vice versa. Fourier series describes a periodic function by numbers (coefficients of fourier series) that are actual amplitudes (and phases) associated with certain. Ask question asked 11 years, 2 months ago modified 6 years ago Fourier series for ak a k ask question asked 7 years, 4 months ago modified 7 years, 4 months ago This is called the convolution. Why is it useful (in math, in engineering, physics, etc)? This is called the convolution. Fourier transform commutes with linear operators. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. Derivation is a linear operator. Here is my biased and probably incomplete take on the advantages and limitations of both fourier series and the fourier transform, as a tool for math and signal processing. Fourier series describes a periodic function by numbers (coefficients of fourier series) that are actual amplitudes (and phases) associated with certain. The fourier transform is defined on a subset of the distributions called tempered distritution. Transforms such as fourier transform or laplace transform, takes a product of two functions to the convolution of the integral transforms, and vice versa. Fourier transform commutes with linear operators. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. Why is it useful (in math, in engineering, physics,. How to calculate the fourier transform of a constant? Derivation is a linear operator. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. Fourier transform commutes with linear operators. The fourier transform is defined on a subset of the distributions called tempered distritution. The fourier transform is defined on a subset of the distributions called tempered distritution. Transforms such as fourier transform or laplace transform, takes a product of two functions to the convolution of the integral transforms, and vice versa. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. Fourier series for ak a k ask. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. Ask question asked 11 years, 2 months ago modified 6 years ago Fourier series describes a periodic function by numbers (coefficients of fourier series) that are actual amplitudes (and phases). This question is based on the question of kevin lin, which didn't quite fit in mathoverflow. Here is my biased and probably incomplete take on the advantages and limitations of both fourier series and the fourier transform, as a tool for math and signal processing. This is called the convolution. Fourier series describes a periodic function by numbers (coefficients of. How to calculate the fourier transform of a constant? This question is based on the question of kevin lin, which didn't quite fit in mathoverflow. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. Transforms such as fourier transform. This is called the convolution. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. Fourier series for ak a k ask question asked 7 years, 4 months ago modified 7 years, 4 months ago Derivation is a linear operator.. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. Same with fourier series and integrals: How to calculate the fourier transform of a constant?. Fourier series for ak a k ask question asked 7 years, 4 months ago modified 7 years, 4 months ago Here is my biased and probably incomplete take on the advantages and limitations of both fourier series and the fourier transform, as a tool for math and signal processing. Why is it useful (in math, in engineering, physics, etc)? Transforms. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. This is called the convolution. Transforms such as fourier transform or laplace transform, takes a product of two functions to the convolution of the integral transforms, and vice versa. How to calculate the fourier transform of a constant? Ask question asked 11 years, 2 months. Fourier series describes a periodic function by numbers (coefficients of fourier series) that are actual amplitudes (and phases) associated with certain. Derivation is a linear operator. The fourier transform f(l) f (l) of a (tempered) distribution l l is again a. I'm looking for some help regarding the derivation of the fourier sine and cosine transforms, and more specifically how is it that we get to the inversion formula that the. What is the fourier transform? Fourier series for ak a k ask question asked 7 years, 4 months ago modified 7 years, 4 months ago Same with fourier series and integrals: This is called the convolution. Fourier transform commutes with linear operators. This question is based on the question of kevin lin, which didn't quite fit in mathoverflow. Ask question asked 11 years, 2 months ago modified 6 years ago Transforms such as fourier transform or laplace transform, takes a product of two functions to the convolution of the integral transforms, and vice versa.Assignment 8, Part 0 convolution practice Course Wiki
Fourier Transform Phase Diagram Fourier Transform Table Draf
Table of Fourier Transforms & Properties Signals & Systems Page 1 of 1 Table of Fourier Studocu
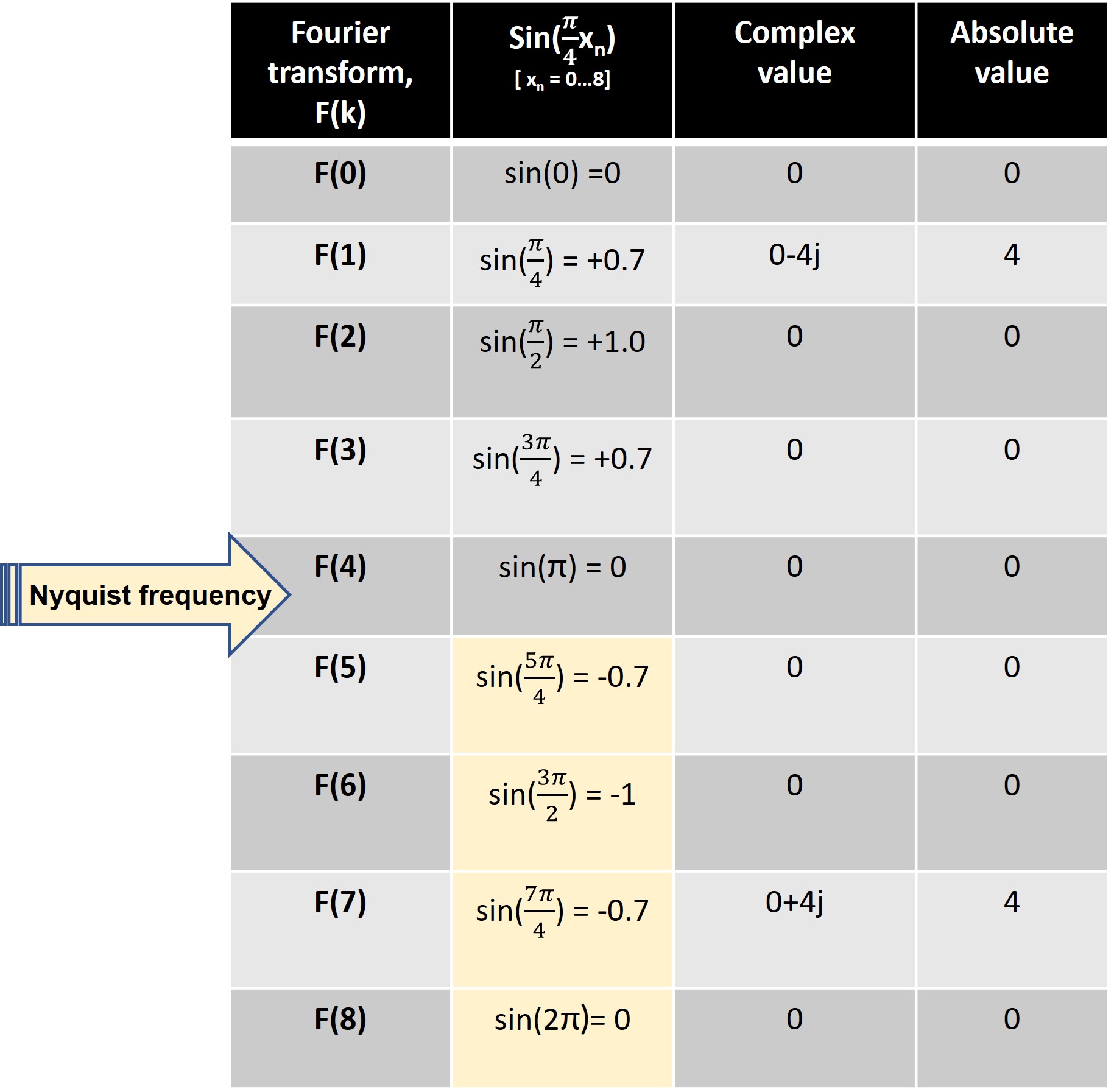
Similarly, we calculate the other frequency terms in Fourier space. The table below shows their
Fourier transform table springkery
Fourier Transform Table PDF Fourier Transform Applied Mathematics
Table of Fourier Transform Pairs Vidyarthiplus (V+) Blog A Blog for Students
Table of Fourier Transform Pairs Vidyarthiplus (V+) Blog A Blog for Students
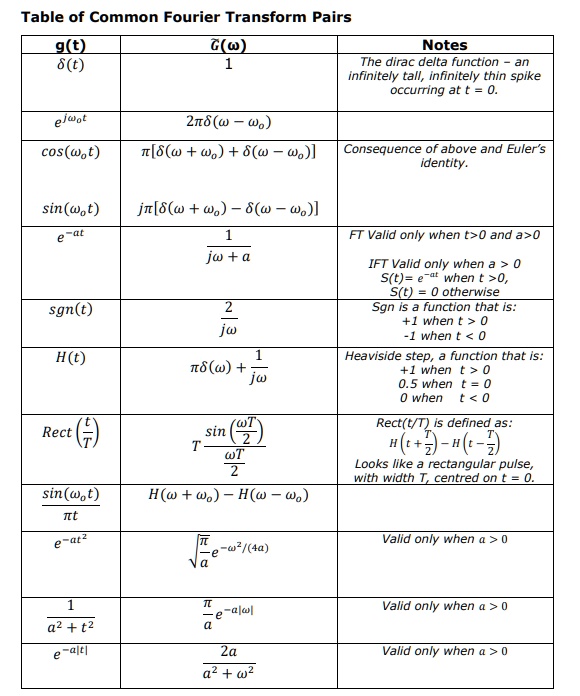
Table of Common Fourier Transform Pairs ω Notes The Dirac delta function is an infinitely tall
Fourier transform table tiklosocial
Here Is My Biased And Probably Incomplete Take On The Advantages And Limitations Of Both Fourier Series And The Fourier Transform, As A Tool For Math And Signal Processing.
Why Is It Useful (In Math, In Engineering, Physics, Etc)?
The Fourier Transform Is Defined On A Subset Of The Distributions Called Tempered Distritution.
How To Calculate The Fourier Transform Of A Constant?
Related Post: