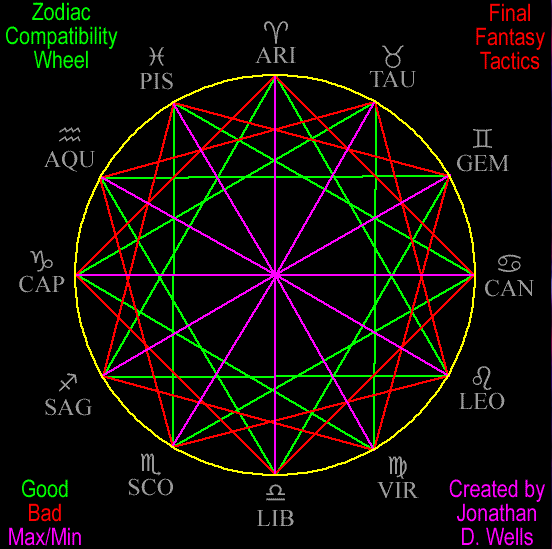
Fft Zodiac Chart

Fft Zodiac Chart - Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。 Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递. 为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正.

Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。 Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正. 而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递.

FFXII zodiac chart, Final fantasy tattoo, Final fantasy xii, Final fantasy

In final fantasy tactics is there a easy way to build a team based off zodic signs? r

为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。

Final Fantasy Tactics Part 1 Orbonne Monastery

而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。

Best compatibility comp possible with Ramza as capricorn r/finalfantasytactics

Fft Zodiac Chart A Visual Reference of Charts Chart Master

Made a couple FFT infographics (map + zodiac reference) r/finalfantasytactics

Astrological Signs Compatibility Chart

Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递. 为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。

Made a couple FFT infographics (map + zodiac reference) r/finalfantasytactics

而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递. 为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。 Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。

FFT Zodiac Wheel by MaxTheBird on DeviantArt

为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正. Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。 Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递.

Final Fantasy Tactics Best Zodiac Sign for Ramza + Compatibility Explained YouTube

Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。 Fft“分辨率带宽”不应与屏幕上显示的“fft 分辨率” 数字（153 khz）相混淆。后者描述的是 fft 数据中两个 fft 点之间的实际间隔，但它不是在既定时间跨度内所获得的实际分辨率带宽。而参考前述示意图，当 n=2^ {l} 时，奇偶分离后的快速傅里叶变换（ n 点 fft ）包含 l 级，每级进行 n/2 次复数乘法和 n 次加法运算，显然计算得到了简化。奇偶分离的过程天然适用于递. 为什么fft变换后的幅值感觉不对？请看一下问题出在哪里（matlab环境）。 [图片] 原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正.